路径规划之图搜索算法

基于此文章学习整理。

配置空间(Configuration Space)

在实际环境，也就是机器人的工作空间(Workspace)中，机器人是有形状和大小的，这不利于进行运动规划。要将工作空间转换到配置空间中，即将机器人转化为一个质点，同时将障碍物按照机器人的体积进行膨胀，如下图：

图搜索算法的基本流程

创建一个容器，用来存储将要访问的节点

将起点加入容器

开始做如下循环

从容器中取出一个节点

获得该节点的邻节点

将这些邻节点装入容器

结束循环

深度优先搜索(DFS)

通过栈(Stack)数据结构实现深度优先搜索，如下图所示：

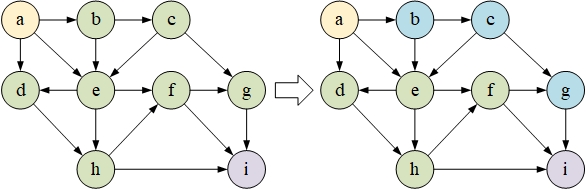
将该算法应用到路径规划中，如下图所示：

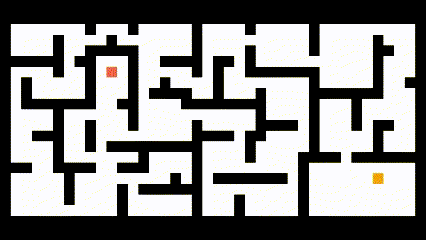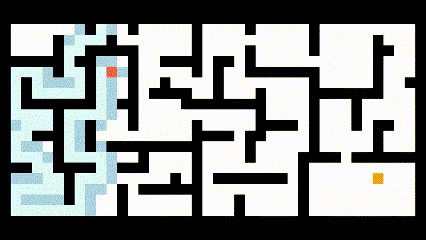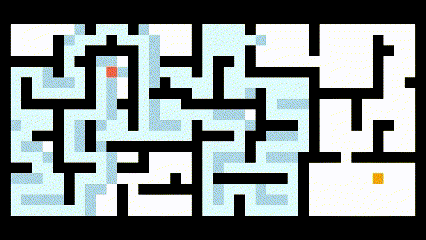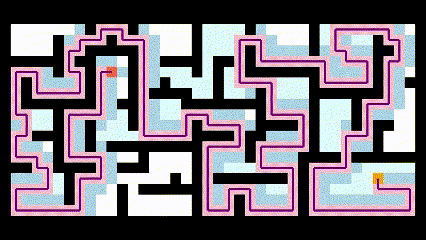
可见该算法所得到的路径并不是最短路径。

广度优先搜索(BFS)

通过队列(Queue)数据结构实现广度优先搜索，如下图所示：

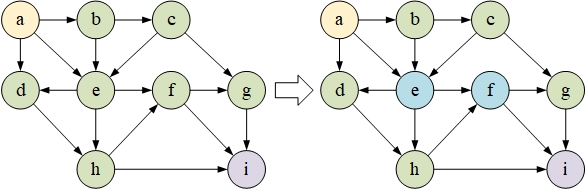
将该算法应用到路径规划中，如下图所示：

可见该算法所得到的路径为最短路径，但是需要大量时间。

贪婪最佳优先算法(GBFS)

GBFS使用的是优先队列(Priority Queue)，普通队列是一种先进先出的数据结构，而在优先队列中元素被赋予了优先级，最高优先级元素优先弹出。

在图搜索算法中，使用代价函数$f\left(n\right)$$f\left( n \right)$作为优先级判断标准，$f\left(n\right)$$f\left( n \right)$越小，优先级越高。GBFS使用启发评估函数$h\left(n\right)$$h\left( n \right)$作为代价函数，$h\left(n\right)$$h\left( n \right)$为当前节点到终点的代价，一般用欧氏距离(Euclidean Distance)或者曼哈顿距离(Manhattan Distance)表示。

其中，欧氏距离和曼哈顿距离分别表示如下：

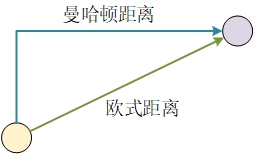
欧式距离和曼哈顿距离的计算方法分别为：

$D_{\text{Manhattan}}=\left|x_1-x_2\right|+\left|y_1-y_2\right|$${D_{{\text{Manhattan}}}} = \left| {{x_1} - {x_2}} \right| + \left| {{y_1} - {y_2}} \right|$

$D_{Euclidean}=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}$${D_{Euclidean}} = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}$

在无障碍物的地图中，GBFS可以很快的找到最短路径，如下图所示：

但是在实际情况中，很容易陷入局部最优陷阱，找不到最短路径：

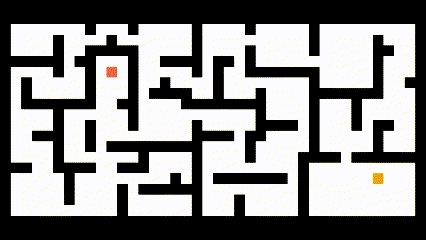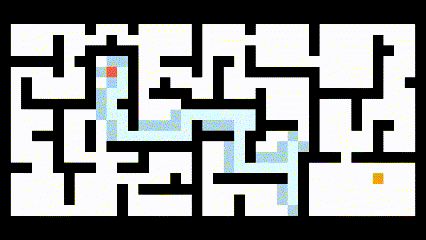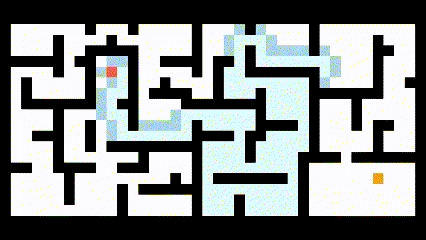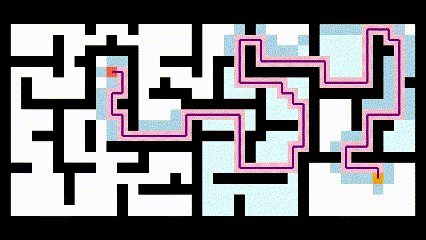
将该算法应用到路径规划中，如下图所示：

Dijkstra算法

Dijkstra算法可以用于有权图的图搜索，Dijkstra算法与GBFS同样使用优先队列的数据结构，不过其代价函数$g\left(n\right)$$g\left( n \right)$定义为从起点到当前点的移动代价，如下图所示：

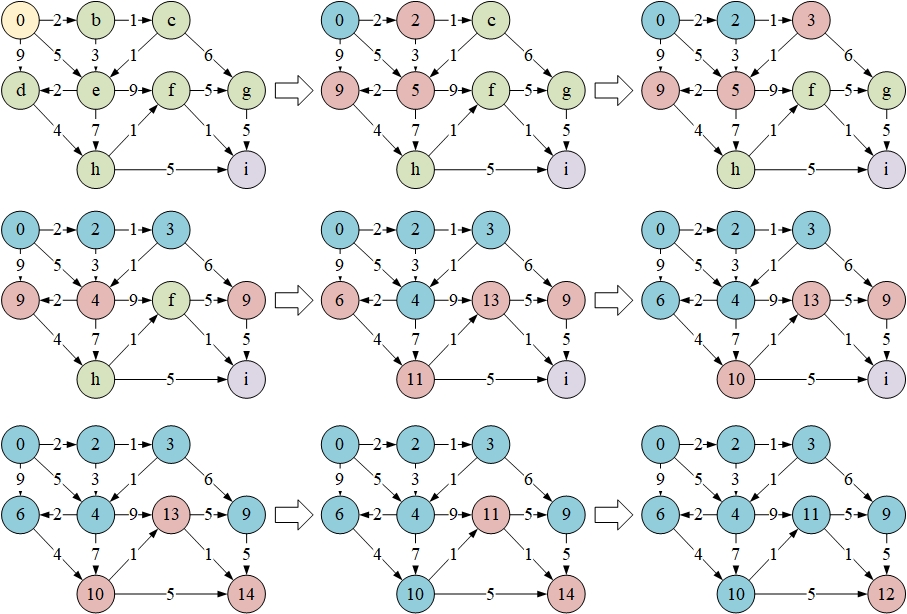
将该算法应用到路径规划中，如下图所示：

Dijkstra算法和BFS算法一样可以得到最短路径，但是速度较慢。

A*算法

在A*算法中，将GBFS与Dijkstra算法的代价函数进行了结合，即

$f\left(n\right)=h\left(n\right)+g\left(n\right)$$f\left( n \right) = h\left( n \right) + g\left( n \right)$

由于引入启发函数$h\left(n\right)$$h\left( n \right)$，A*算法得到的路径不一定是最优的。但是当对所有的节点$n$$n$，都有

$h\left(n\right)<h^{\ast }\left(n\right)$$h\left( n \right) < {h^ * }\left( n \right)$

其中，$h^{\ast }\left(n\right)$${h^ * }\left( n \right)$为从节点$n$$n$到目标节点的真实代价时，A*算法得到的路径是最优的。

将该算法应用到路径规划中，如下图所示：

权重A*算法

将A*算法中的代价函数更新如下：

$f\left(n\right)=g\left(n\right)+\epsilon h\left(n\right),\epsilon >1$$f\left( n \right) = g\left( n \right) + \varepsilon h\left( n \right),\varepsilon > 1$

当$\epsilon$$\varepsilon$为1时，该代价函数为A*算法的代价函数，$\epsilon$$\varepsilon$越大，权重A*算法越接近GBFS，可以理解为通过牺牲一定的最优性，以换取搜索速度。

提高A*算法效率的方法

A*算法在某些情况下会出现低效率的情况，其中的一种情况是在大型的开放空间中搜索，如下图所示：

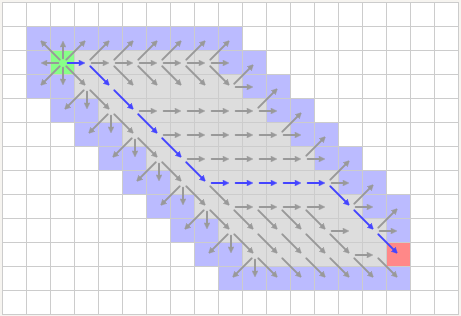
可以看见图中的每一条路径的代价都是相同的，即，A*算法在搜索过程中搜索了许多不必要的点。

可以用以下几种方法提高A*算法的效率：

1. 让$h\left(n\right)$$h\left( n \right)$尽可能地接近$h^{\ast }\left(n\right)$${h^ * }\left( n \right)$

2. 轻微地干扰$h\left(n\right)$$h\left( n \right)$

   $$\begin{array}{}\text{(1)}& \tilde{h}\left(n\right)=h\left(n\right)\times \left(1+p\right)p<\frac{\text{minimum cost of one step}}{\text{expected maximum path cost}}\end{array}$$

跳点搜索算法(JPS)

Look Ahead Rule

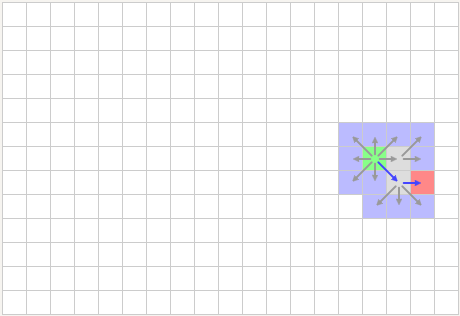
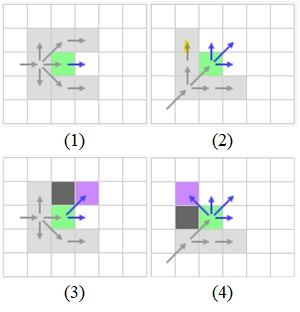
• 如下图中图(1)所示，当水平或竖直搜索时，根据Look Ahead Rule，仅需要考虑一个节点(natural neighbors)

• 当如图(2)所示进行对角线搜索时，需要考虑三个节点

• 当出现如图(3)、(4)所示的特殊情况时，需要额外多考虑一个紫色节点(forced neighbors)

Jumping Rules

在没有搜索到终点的情况下：

• 首先如图(1)所示水平或竖直搜索，直到遇到如图(3)所示情况，并将图三中紫色节点作为Jump Point Successor，加入优先队列

• 如果水平或竖直搜索都没有找到Jump Point Successor，则进行如图(2)所示的对角线搜索，直到遇到如图(4)所示情况，并将图三中紫色节点作为Jump Point Successor

• 将找到Jump Point Successor节点的节点列为Jump Point，并继续搜索，如果没有新的forced neighbor，从队列中的节点继续搜索。

JPS演示

1. 示例1

   

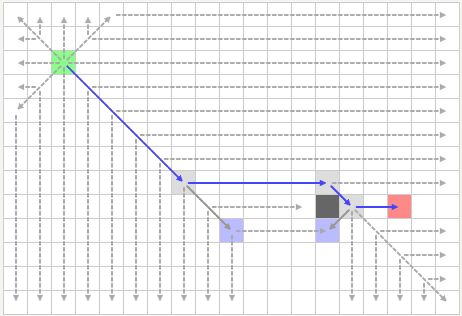
2. 示例2：在开放空间搜索时与A*算法比较

   

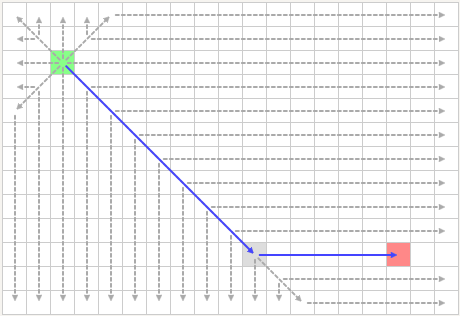
3. 示例3：JPS是否总是最优？

   下图为JPS算法得到的路径

   

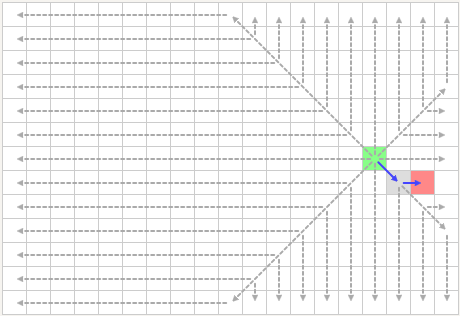
   下图为A*算法得到的路径